10_Circuiti-aritmetici

Questo file è la rielaborazione delle slide 10_Circuiti-aritmetici.pdf

---

La somma tra due numeri binari avviene in questo modo: Il riporto in uscita della somma precedente viene assegnato come riporto in entrata alla somma successiva. Questo tipo di addizioni vengono fatte continuamente all’interno della nostra macchina, e questo viene fatto attraverso gli addizionatori, esistono vari tipi di addizionatore:

• Half adder: Un circuito molto semplice che fa la somma di 2 bit (calcolando il riporto in uscita) senza considerare alcun riporto in ingresso. Ha 2 uscite:
  • Somma: $S=A\oplus B$ ovvero l’uscita di una porta XOR
  • Riporto: $C=A\cdot B$ ovvero l’uscita di una porta AND Di seguito la rappresentazione grafica di questo circuito:
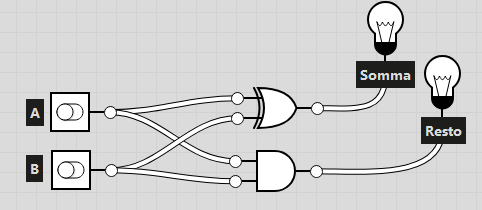
• Full adder: anche chiamato addizionatore ad 1 bit può essere espresso da 2 funzioni logiche a tre ingressi, i due bit da sommare (chiamati in seguito $A$ e $B$) e l’eventuale riporto in entrata (chiamato in seguito $C_{in}$):
  • Somma: calcola la somma tra i 2 bit in entrata ed il riporto in ingresso, usando questa formula: $S=A\oplus B\oplus C_{in}$ praticamente una porta XOR a tre ingressi.
  • Riporto: La seconda funzione logica calcola il riporto in uscita, usando questa formula: $C_{out}=(x_i\times c_i)+(y_i\times c_i)+(x_i\times y_i)$ Di seguito la tabella di verità e la rappresentazione grafica del circuito:
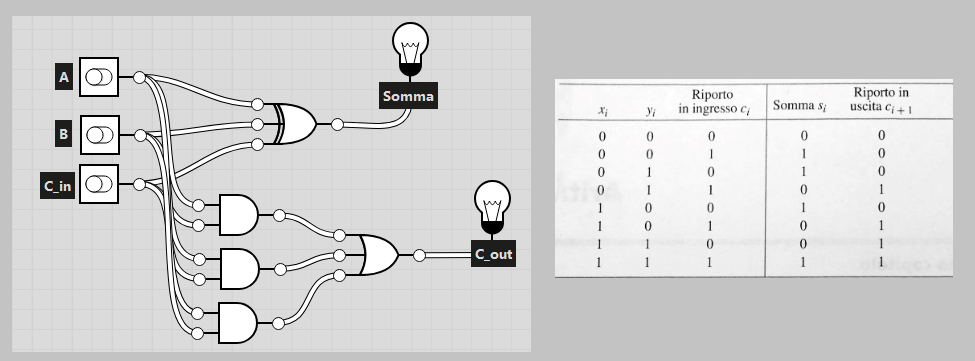
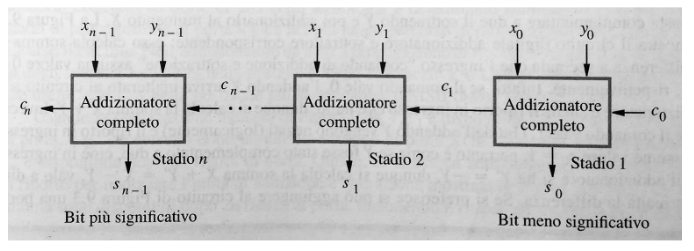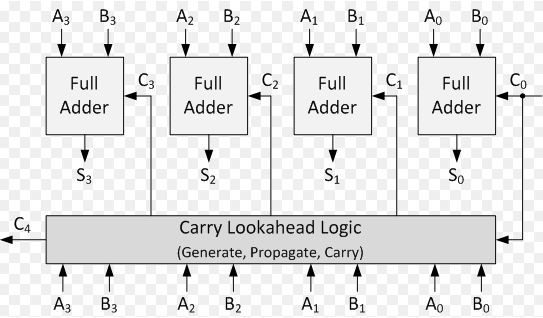
• Ripple carry adder: anche chiamato addizionatore con propagazione di riporto, si ottiene collegando tra di loro diversi full-adder in modo da propagare il riporto, di seguito la rappresentazione grafica: Il problema principale di questo addizionatore è che ogni full adder per andare avanti devo aspettare il calcolo del resto dell’adder precedente, questo crea dei rallentamenti. Il termine “ripple” indica che il riporto si propaga sequenzialmente da un bit al successivo, come un’onda.
• Carry lookahaed adder: per risolvere il problema del ripple carry adder nasce questo tipo di addizionatore, che va a calcolare il resto in parallelo propagandolo in base a delle formule matematiche (funzioni $G_i$ e $P_i$ spiegato in seguito), tutto ciò lo rende più veloce e quindi viene ancora oggi usato dentro le ALU dei processori.

Trabocco (Overflow)

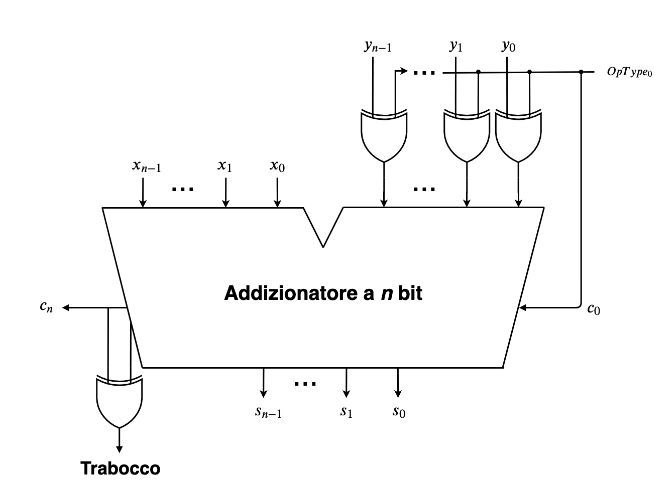
Si parla di trabocco quando andiamo a sommare dei bit e il risultato dell’operazione aritmetica è un numero che supera le capacità di rappresentazione del circuito. Il trabocco avviene molto spesso nelle operazioni algebriche dove si prendono in considerazioni numeri con segno.

• Addizionatore algebrico: è un circuito logico che somma due numeri binari a n bit, considerando anche il segno, la parte importante per questo circuito è la gestione dell’Overflow, infatti viene calcolato utilizzando questo formula: $c_n\oplus c_{n-1}$ con $c_n$ che sarebbe il riporto generato dall’ultimo bit, e $c_{n-1}$ il riporto generatore dal penultimo bit, in pratica se il risultato di questa formula ci da 1 c’è stato un trabocco.

---

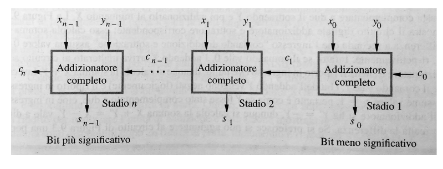
Ripple Carry Adder e Calcolo del Ritardo Il ritardo totale del circuito dipende dal percorso più lento.

• In un Full Adder (FA):
  • La somma parziale è calcolata dopo 1 ritardo di porta:
    $s_i=x_i\oplus y_i\oplus c_i$
  • Il riporto è calcolato dopo 2 ritardi di porta:
    $c_{i+1}=x_i{y}_i+x_i{c}_i+y_i{c}_i$
• In un Ripple Carry Adder a $n$ bit:
  • L’ultimo riporto è calcolato dopo $2n$ ritardi di porta.
  • L’ultimo bit di somma è calcolato dopo $2n-1$ ritardi di porta.

---

Funzioni di Generazione e Propagazione Riscrivendo: $c_{i+1}=x_i{y}_i+(x_i+y_i)c_i$ introduciamo:

• Funzione di generazione: $G_i=x_i{y}_i$
• Funzione di propagazione: $P_i=x_i+y_i$ Il riporto diventa: $c_{i+1}=G_i+P_i{c}_i$ questa formula ci avvantaggia perché $G_i$ e $P_i$ dipendono solo dagli ingressi $x_i$ e $y_i$ e possono essere calcolati in parallelo.

---

Carry lookahaed adder a 2 livelli: Per ridurre ulteriormente il tempo di calcolo si utilizza una struttura a più livelli logici, in pratica si prende la struttura di Carry lookahaed adder e la si estende su due livelli.

---

Circuito moltiplicatore sequenziale: gli addizionatori vengono anche utilizzati per fare le moltiplicazioni, infatti la moltiplicazioni di numeri senza segno può essere realizzata usando un addizionatore ad n bit e due registri.

A = 0
Q = Moltiplicatore
M = Moltiplicando

Per n cicli:
	se q[0] = 1:
		A = A + M
	altrimenti:
		A = A + 0
	c = riporto
	A scorre verso destra di una posizione
	Q scorre verso destra di una posizione
	c scorre verso destra di una posizione

Alla fine del ciclo concatenando i contenuti di A e Q si otterrà il prodotto finale

---

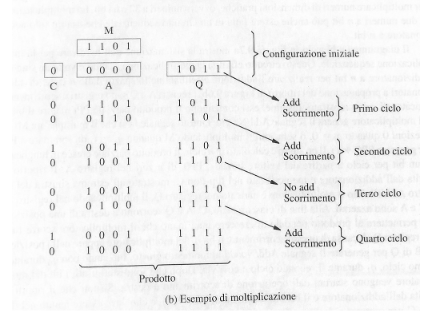
Moltiplicazione dei numeri con segno: per i numeri con il segno la situazione si complica un po’, usiamo l’algoritmo di Booth: L’algoritmo di Booth è un metodo efficiente per moltiplicare numeri binari con segno in complemento a due. L’idea chiave è ricodificare il moltiplicatore come somme e sottrazioni di potenze di 2. Nel caso semplice in cui il moltiplicatore contiene una sequenza contigua di 1, Il prodotto è uguale al moltiplicando fatto scorrere di 5 posizioni a sinistra + il complemento a 2 del moltiplicando fatto scorrere di 1 posizione a sinistra.

---

Ricodifica bit-pair Il ricodifica Bit-pair è una tecnica di compressione dei dati utilizzata per ridurre la lunghezza di una sequenza di bit senza perdere informazioni questo lo fa raggruppando i bit in coppia (bit pair) e li codifica in un nuovo formato.

---

Divisione con ripristino: anche questo tipo di circuito viene realizzato usando un addizionatore n+1 bit, un registro($M$) e 2 shift register ($A$ e $Q$), questi componenti vengono usati dentro un ciclo che esegue $n$ volte i seguenti passaggi:

• Fare scorrere $A$ e $Q$ a sinistra di una posizione
• Sottrarre $M$ da $A$ e porre il risultato in $A$
• Se il segno di $A$ è 1, porre $q_0$ a 0 e sommare $M$ ad $A$; altrimenti, porre $q_0$ a 1 All’inizio $M$ contiene il Divisore, $A$ contiene 0 e $Q$ contiene il Dividendo Alla fine $A$ contiene il Resto e $Q$ contiene il Quoziente

---

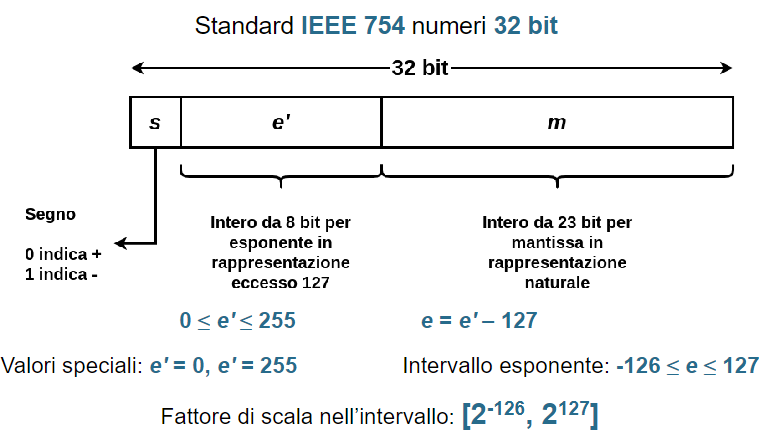
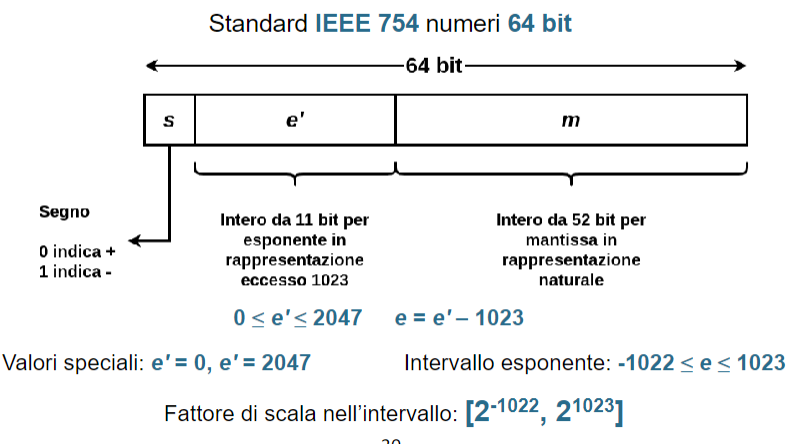
Numeri in virgola mobile: un numero in binario con virgola mobile viene rappresentato da:

• Un segno $s$ per il numero
• La mantissa $m$
• Un esponente $e$ con segno in base 2